CONJUNTOS Y SU RELACION CON LA VIDA DIARIA

CONJUNTOS


Es una colección de objetos, bien determinados, es decir que, dado un objeto y un conjunto, se puede establecer si el objeto pertenece o no al conjunto.


Observaciones:
Cada
objeto del conjunto se llama elemento.
Los conjuntos se nombran con letras mayúsculas.
Se representan en diagramas de Venn.
Los elementos se encierran entre llaves.


A = {a, e , i , o , u}












DETERMINACIÓN DE CONJUNTOS


Los conjuntos se pueden determinar por extensión y por comprensión.
Extensión: Cuando se nombra cada elemento que lo integra. Ejemplo: El conjunto de los números naturales impares mayores que 5. M={7, 9, 11, 13, 15, . . . }
Comprensión: Cuando se recurre a la propiedad que lo caracteriza y que sólo cumplen sus elementos; Ejemplo: El conjunto de los números naturales impares mayores que 5. M={ x ϵ N / x= 2n + 5}


Ejercicio: Determinar por extensión y comprensión cada uno de los siguientes conjuntos:

El conjunto de los números primos menores que 35.
El conjunto de los cuadrados perfectos menores que 100.
El conjunto de los números enteros que dividen a -8.

Conjunto vacío.
Conjunto infinito.
Conjunto finito.
conjunto universal.


RELACIÓN DE PERTENENCIA


Un elemento pertenece a un conjunto si cumple con las características que definen al conjunto. En el ejemplo 1: 7 ϵ M. Se lee 7 pertenece a M.


2 Ɇ M. Se lee 2 no pertenece a M.


Ejemplos: T = {x ϵ Q / -1 < x < 7}, determina el valor de verdad.


a) -0,15 ϵ T


b) -4/3 ϵ T


c) 7 ϵ T


d) {3} ϵ T


OBSERVACIONES

En un conjunto no se repiten elementos. Sup M={a,a,a}={a}.
En un conjunto no importa el orden en que se coloquen los elementos. B = {a,b} = {b,a}.
Para el desarrollo de la teoría de conjunto deben darse las siguientes condiciones:



Un conjunto universal.
Determinar el conjunto por comprensión.
Determinar el conjunto por extensión.


4. El conjunto vacío es subconjunto de todo conjunto.


Ejemplos: Dado el conjunto A = {1,2,{3},4,{5,6}}, indicar cuáles de las siguientes proposiciones son verdaderas y cuáles falsas.


a) 2 ϵ A ___


b) 3 ϵ A ___


c) {5,6} ϵ A ___


d) 6 ϵ A ___


RELACIÓN DE IGUALDAD


Dos conjuntos A y B son iguales si tienen exactamente los mismos elementos.


En símbolos A = B <=> (x ϵ A => x ϵ B) ^ (x ϵ B => x ϵ A)


Es decir: Todo elemento de A pertenece a B y todo elemento de B pertenece a A.


Ejemplo: Determinar si los conjuntos U y V son iguales.


U={x/x ϵ N ^ √x < 4}


V = {0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16}


Solución: U = V


Responder: Q = {1,2} y R = {1,1,2,1,2}. Es cierto que Q = R.


INCLUSIÓN O SIBCONJUNTO


B = {1,2,3,4,5,6,7,8} y A = {2,3,6,8}


Todos los elementos de A son también de B. Decimos entonces que “A está incluido en B” o que “A es subconjunto de B”. A C B.


Definición: Sean A y B dos subconjuntos. Decimos que A es subconjunto de B, A C B, si y sólo si todo elemento de A es también elemento de B, simbólicamente A C B <=> Para todo x (x ϵ A=> x ϵ B).





PROPIEDADES
El conjunto vacío es subconjunto de todo conjunto. Si A es un conjunto cualquiera, entonces φ C A.
Todo conjunto es subconjunto de sí mismo, es decir, si A es cualquier conjunto entonces A C A.
Si A es subconjunto de B, no necesariamente B es subconjunto de A.





4. A C B y B C C, entonces A C C.





Ejercicios: Dado el conjunto A = {1,2, {1,2},3,{4}}, responder falso o verdadero, a las siguientes proposiciones:
{1,2} ϵ A ___
3 C A ___
3 ϵ A ___
{1,2,{4}} C A ___
{1,2} C A ___
{3} C A ___
{1,2,3} ϵ A ___
{3,{4}} ϵ A ___


Dado que el siguiente siagrama, subrayar las proposiciones que sean verdaderas.



A C U ___
B C U ___
C C B ___
B C B ___
B C A ___
A C C ___
C C A Ȼ B ___


OPERACIONES ENTRE CONJUNTOS


La unión entre los conjuntos A y B es el conjunto formado por los elementos que pertenecen a A o a B. Se representa A U B.


Simbólicamente A U B = {x/x ϵ A v x ϵ B}


Ejemplo: A = {1,2,3,4} y B = {3,4,5,6,7,}
{1,2} son exclusivos de A
{5,6,7} son exclusivos de B
{3,4} pertenecen a los dos conjuntos
A U B = {1,2,3,4,5,6,7}


PROPIEDADES DE LA UNIÓN
P.1 Idempotencia. A U A = A
P.2 Identidad. A U φ = A ; A u U = U
P.3 Conmutativa. A u B = B u A
P.4 Asociativa. A u (B u C) = (A u B) u C
P.5 A C (A u B)


DIAGRAMAS DE VENN DE LA UNION


DISYUNTOS: A y B son conjuntos disyuntos, cuando no tienen elementos en común:
A U B = φ


NO DISYUNTOS:



A U B ≠ φ


IGUALES:



A U B = A= B


SUBCONJUNTOS:





A U φ = A






INTERSECCIÓN ENTRE CONJUNTOS


Se llama intersección de dos conjuntos A y B al conjunto formado por los elementos que pertenecen simultáneamente a A y B.


Se representa A ∩ B.


Simbólicamente A ∩ B = {x/x ϵ A ^ x ϵ B}


Si A ∩ B es vacío se dice que A y B son conjuntos disyuntos. A ∩ B = φ


PROPIEDADES DE LA INTERSECCIÓN

P.1 Idempotencia. A ∩ A = A
P.2 Identidad. A ∩ φ = φ ; A ∩ U = A
P.3 Conmutativa. A ∩ B = B ∩ A.
P.4 Asociativa. A ∩ (B ∩ C) = (A ∩ B) ∩ C.


Ejemplo: A = {1,2,3,4} y B = {3,4,5,6}


A ∩ B = {3,4}


DIAGRAMAS DE VENN DE LA INTERSECCIÓN


1) Intersecantes:








2. Disyuntos:



B ∩ C = φ


3. Iguales:



A ∩ B = A = B


4. Subconjuntos





A ∩ B = B


LA DIFERENCIA ENTRE CONJUNTOS


La diferencia entre dos conjuntos A y B es el conjunto formado por los elementos que pertenecen a A y no pertenecen a B. Se representan A – B.


Simbólicamente: A – B = {x/x ϵ A ^x Ɇ B }


Ejemplo: A = {1,2,3,4} y B = {3,4,5,6} => A – B = {1,2}


PROPIEDADES DE LA DIFERENCIA
P. 1 A – B = A ∩ B’
P. 2 A – B ≠ B – A
p.3 A – A = φ
p.4 U – A = A’





CONJUNTO UNIVERSAL


Es el conjunto formado por todos los elementos de tema en referencia. Se representa con U.





COMPLEMENTO DE UN CONJUNTO


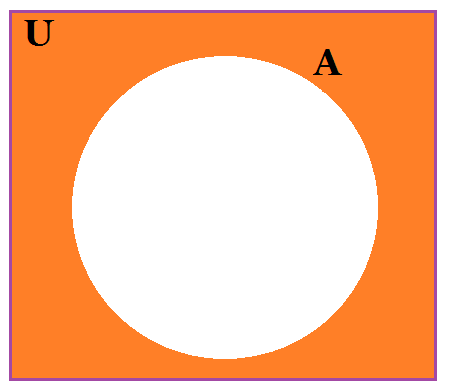
El complemento de un conjunto A con respecto al conjunto universal U es el conjunto formado por los elementos de U que no pertenecen a A.


El complemento de A se simboliza A’ y se lee: A complemento.


Simbólicamente A’ = U – A = {x/x ϵ U ^x Ɇ A}





PROPIEDADES DEL COMPLEMENTO
P.1 (A’)’ = A ———————-> complemento del complemento de A es A
P.2 A u A’ = U
P.3 A ∩ A’ = φ
P.4 Leyes de Morgan: (A u B)’ = A’ ∩B’ ; (A ∩ B)’ = A’ u B’


Ejemplo:


U = {1,2,3,4,5,6,7} y A = {2,3,5}


A’ = U – A = {1,4,6,7}


Halar A’
U = {1,2,3,4,5,6, . . . , 19,20}
A = {1,2,3,6,9,18}
A’ = {4,5,7,8,10,11,12,13,14,15,16,17,19,20}






DIFERENCIA SIMÉTRICA


La diferncia simétrica entre dos conjuntos A y B es el conjunto formado por los elementos que pertenecen a: A u B u no pertenecen a A ∩ B. Se representa por A Δ B.


Simbólicamente : A Δ B = (A u B) – (A ∩ B)


X ϵ (A Δ B) <=> x ϵ (A u B) ^x Ɇ (A ∩ B)


A Δ B = {x/x ϵ (A u B) ^x Ɇ (A ∩ B)}


PROPIEDADES DE LA DIFERENCIA
P.1 A Δ B = B Δ A
P.2 A Δ φ = φ
P.3 A Δ B = (A u B) – (A ∩ B)


Ejemplos generales: Dados los conjuntos:
U = { x/ -3 < x < 10 ; x ϵ Z }
A = {x/ 1< x < 8 ; x ϵ Z }
B = {x/ -3< x < 5 ; x ϵ Z}
C = {x/ 2 < x < 9 ; x ϵ Z}


Hallar:
A – (C ‘ ∩ B) = {2,3,4,5,6,7,8}
(C u A) ∩ B = {-3,-2,-1,2,3,4}
B’ – (B Δ C) = {5,6,7,8,10}


Ejercicio Propuesto: Dado los conjuntos:
U = {x/x -5 < x < 10 ; x ϵ Z}
A = {x/x -1 < x < 8 ; x ϵ Z}
B = {x/x 4 < x < 9 ; x ϵ Z}
C = {x/x 1 < x < 6 ; x ϵ Z}


Hallar:
B – (A ∩ C ‘)
A’ ∩ (C – B)
(A – B) ∩ (C ‘ u B’)


CARDINAL DE UN CONJUNTO


El cardinal de un conjunto es el número de elementos que posee. El cardinal del conjunto A se simboliza n(A): Se lee: número de elementos de A


A = {1,2,3,4} y B = {3,4,5,6,7} ; n(A) = 4 y n(B) = 5
n(A u B) = 7
n (A ∩ B) = 2


Luego n(A u B) = n(A) + n(B) – n (A ∩ B)


En general: n(A u B) = (4 + 5 ) – 2 = 9 – 2 = 7


APLICACIONES DE LA TEORÍA DE CONJUNTOS


CARDINAL O NÚMERO DE ELEMENTOS PARA LA UNIÓN DE DOS CONJUNTOS.


Si A y B son conjuntos diferentes de vacío, entonces:
n(A u B) = n(A) + n(B), si A y B no tienen elementos comunes.
n(A u B) = n(A) + n(B) – n(A ∩ B) si A y B tienen elementos comunes.


Ejemplo 1:
A = {1,3,5}
B = {6,7,8,9}


n(A u B) = n(A) + n(B) = 3 + 4= 7


Ejemplo 2:
A = {-2,-1,0,1,2,3}
B = {2,3,4,5,6}


n(A) = 6 n(B) = 5


A ∩ B = {2,3}


n(A ∩ B) = 2


n(A u B) = n(A) + n(B) – n (A ∩ B)


(6 + 5) – 2 = 11 – 2 = 9


n(A u B) = 9


Ejemplo con tres conjuntos:


n(A u B u C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(A ∩ C) – n(B ∩ C) + n(A ∩ B ∩ C)


Ejemplo: En una encuesta realizada en la corporación de la ciudad a un total de 150 universitarios se hallaron los siguientes datos:
54 estudian lógica
89 estudian Epistemología
80 estudian D
60 estudian D y epistemología
10 estudian lógica solamente
20 estudian lógica y diseno
15 estudian las tres materias simultáneamente
¿ Cuántos estudian lógica y epistemología, pero no diseno?
¿ Cuántos estudian sólo una materia?
¿ Cuántos estudian a lo sumo dos materias?





Se forman únicamente 8 regiones
Los que estudian únicamente lógica. n(R1) = 10
Los que estudian lógica y epistemología. n(R2 y R3) = 5
Los que estudian únicamente epistemología. n (R4) = ?
Los que estudian lógica, epistemología y diseno simultáneamente. n(R3) =15
Los que estudian lógica y diseno. n(R3 y R5) = 20
Los que estudian diseno y epistemología. n(R3y R6)
Los que estudian únicamente diseno. n(R7) = ?
Los que no estudian ninguna de las tres materias.


Para hallar la región 4:


R4 =


Ejemplo 2: En una encuesta realizada en la U de la ciudad a un total de 110 estudiantes en un grupo de actividades extrauniversitarias de las corporación hay suscritos 75 universitarios en música y 35 en teatro. Hallar el número de estudiantes que se dedican a la música y al teatro.
Si las actividades se realizan a la misma hora.
Si las actividades se realizan en días diferentes y se sabe que 15 alumnos están suscritos en ambas.




n(M) = 75
n(T) = 35
n(N ∩ T) = 15
n(U) = 110


A la misma hora:


n(M u T) = n(M) + n(T) – n(M ∩ T)


(75 + 35) – 0 +110


Días diferentes:


n(M u T) = n(M) + n(T) – n(M ∩ T)


(75 + 35) – 15


110 – 15


= 95


Ejemplo 3: La universidad realiza tres tipos de prueba sobre 100 universitarios y anuncia los siguientes resultados:
2 alumnos fracasaron en las tres pruebas
7 alumnos fracasaron en la primera y segunda prueba
8 alumnos fracasaron en la segunda y tercera prueba
10 alumnos fracasaron en la primera y tercera prueba
25 alumnos fracasaron en la primera prueba
30 alumnos fracasaron en la segunda prueba
25 alumnos fracasaron en la tercera prueba
¿ Cuántos aprobaron las tres pruebas?
¿ Cuántos aprobaron en la primera y en la tercera pero no en la segunda?
¿ Cuántos fracasaron en la segunda y tercera pero no en la primera prueba?
¿ Cuántos fracasaron en la segunda y tercera pero no en la primera?
¿ Cuántos fracasaron al menos en dos pruebas?
¿ Cuántos aprobaron al menos una prueba?




Alumnos que fracasaron en las tres pruebas: R5
Alumnos que fracasaron en la primera prueba únicamente: R1
Alumnos que fracasaron en la tercera prueba únicamente: R7
Alumnos que fracasaron en la primera y tercera prueba pero no la segunda: R4
Alumnos que fracasaron en la primera y segunda prueba pero no la tercera: R2
Alumnos que fracasaron en la segunda y tercera prueba pero no la primera: R6
Alumnos que fracasaron en la segunda prueba únicamente: R3
Alumnos que no fracasaron en ninguna prueba: R8
n(R1) + n(R3) + n(R7) = 10 + 17 + 9 = 36


n(U) = n(fracasaaron) + n(No fracasaron)


100 = 100 = Rt + n(No fracasaron)


100 = 47 + n(No fracasaron)


n(No fracasaron = 100 – 47 + 43)
n(R5) = 2
n(R2) = 5
n(R6) = 6
n(R3) = 17
n(R4) = 8
n(R1) = 10
n(R7) = 9
Alumnos fracasados en al menos dos pruebas:


n(R2) + n(R4) + n(R6)


5 + 8 + 6 + 2 = 21
Alumnos que aprobaron al menos una prueba:


n(U) – n(R1) + n(R2) – n(R3)


100 – n(R3)


100-2 = 98